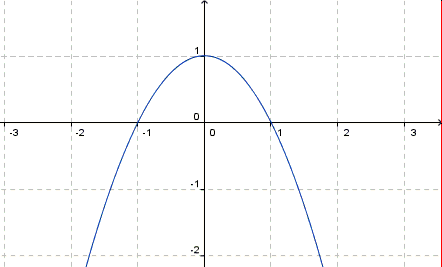
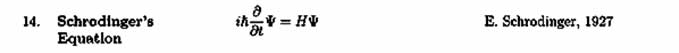Maxwell escogitò un modo per mettere per iscritto ciò che si sapeva al suo tempo sull'elettricità e sul magnetismo, un metodo per compendiare esattamente tutti quegli esperimenti con fili, correnti e magneti. Ecco le quattro equazioni di Maxwell per il comportamento dell'elettricità e del magnetismo nella materia:
 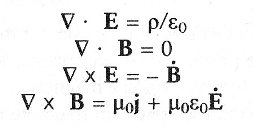 |
|
Arpe nabla ed equazioni di Maxwell nella materia. Legenda:E campo elettrico
B campo magnetico Ė sovrapuntato variazione nel tempo del campo elettrico B sovrapuntato variazione nel tempo del campo magnetico j corrente elettrica
ρ densità delle cariche elettriche ε0 permittività elettrica (o costante dielettrica) μ0 permeabilità magnetica |
| Occorrono alcuni anni di fisica a livello universitario per capire davvero queste equazioni. Esse si scrivono usando una branca della matematica nota come calcolo vettoriale. Un vettore, scritto in grassetto, è una quantità che ha sia una grandezza sia una direzione. Novanta chilometri all'ora non sono un vettore, ma novanta chilometri all'ora sull'autostrada 1 in direzione nord sì. E e B rappresentano il campo elettrico e il campo magnetico. Il triangolo con un vertice verso il basso, chiamato nabla (a causa della sua somiglianza con un tipo di arpa dell'oriente antico), esprime le variazioni dei campi elettrico o magnetico nello spazio tridimensionale. I segni per "prodotto interno" o "prodotto scalare" (rappresentato dal · punto) e per "prodotto esterno" o "prodotto vettoriale" (rappresentato dal segno ×) dopo il nabla, esprimono due diversi tipi di variazione spaziale. Ėsovrapuntato e B sovrapuntato rappresentano la variazione nel tempo, il ritmo di mutamento dei campi elettrico e magnetico. j sta per una corrente elettrica. La lettera greca minuscola ρrho rappresenta la densità delle cariche elettriche, mentre ε0 epsilon con zero e μ0 mu con zero non sono variabili, bensì sono proprietà della sostanza in cui sono misurati E e B, e sono determinate dall'esperimento. In un vuoto, ε0 (permittività elettrica) e μ0(permeabilità magnetica) sono costanti della natura. Se consideriamo quante quantità diverse sono riunite in queste equazioni, sorprende la loro semplicità. Esse avrebbero potuto richiedere pagine e pagine, ma come vediamo non è così. |

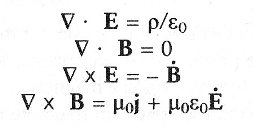
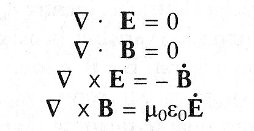
A sx, le equazioni di Maxwell nella materia e a dx le equazioni nel vuoto (oggi, da interdersi come ISM, InterStellar Medium).
Maxwell fissò ρ uguale a zero, per indicare che non ci sono cariche elettriche. Pose uguale a zero anche j, per indicare che non ci sono correnti elettriche. Non eliminò però l'ultimo termine nella quarta equazione, μ0ε0Ė, la debole corrente di spostamento nei materiali isolanti. Perchè no? Come si può vedere dalle equazioni, l'intuizione di Maxwell conservò la simmetria fra i campi magnetico ed elettrico. Persino in un vuoto, nella totale assenza di elettricità, o addirittura di materia, Maxwell suggerì che un campo magnetico variabile suscita un campo elettrico e viceversa.
Le equazioni dovevano rappresentare la natura, e la natura, secondo Maxwell, doveva essere bella ed elegante.
(Per conservare la corrente di spostamento in un vuoto c'era anche un'altra ragione, più tecnica, su cui qui sorvoleremo.)
Questo giudizio, in parte estetico, da parte di un fisico secchione, del tutto sconosciuto tranne che a pochi altri scienziati accademici, ha fatto di più per plasmare la nostra civiltà di dieci presidenti e primi ministri scelti a piacere.


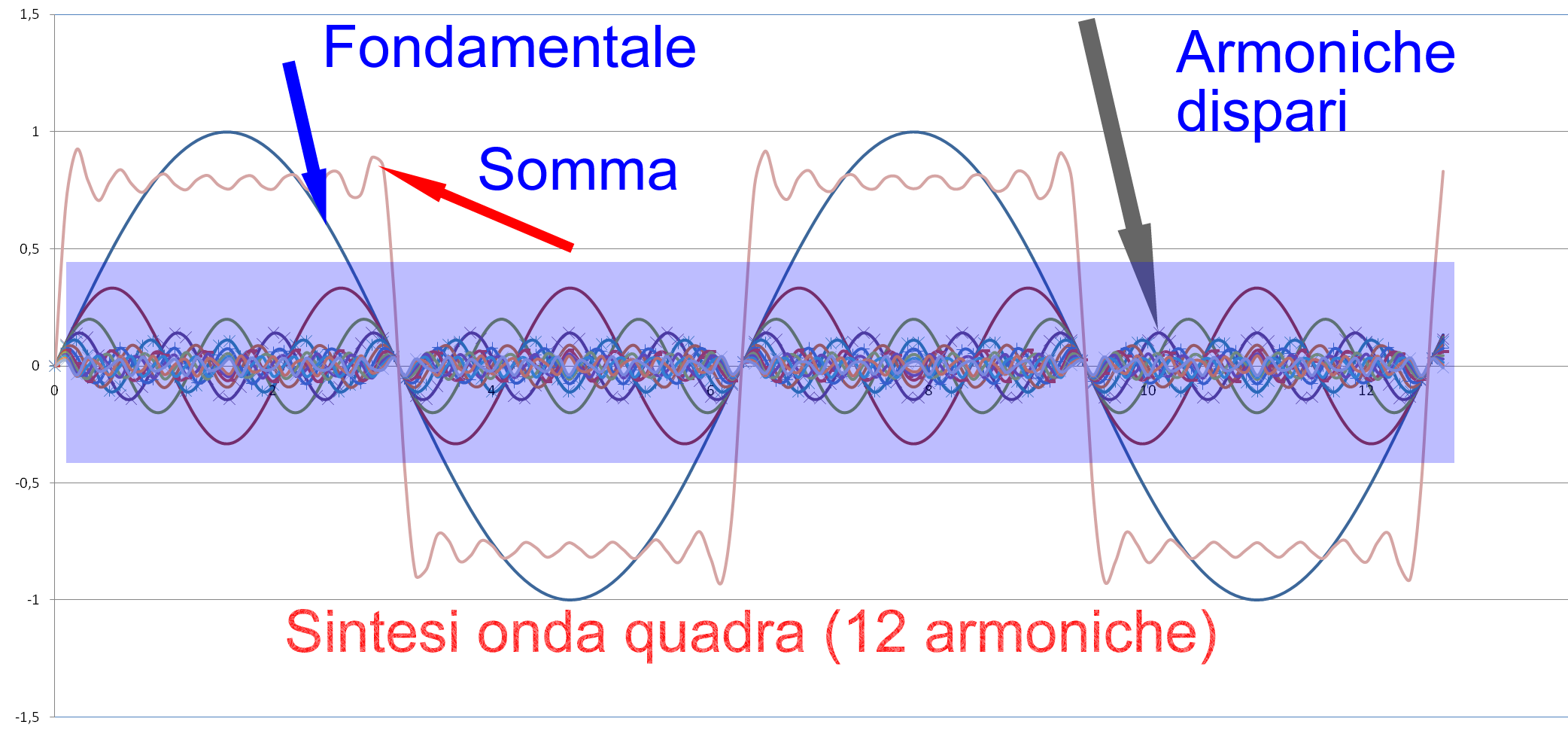
 Vi siete mai chiesti come funzionano i sintetizzatori musicali usati dai gruppi rock? Sentite il suono del moog della PFM in Impressioni di settembre. Come produce quel suono?
Vi siete mai chiesti come funzionano i sintetizzatori musicali usati dai gruppi rock? Sentite il suono del moog della PFM in Impressioni di settembre. Come produce quel suono? 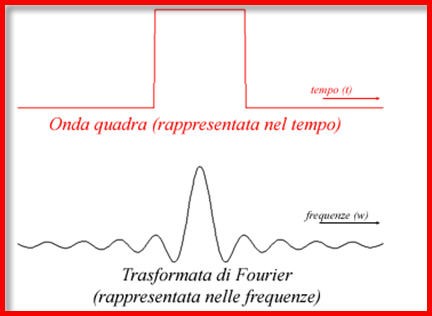 Nel caso in cui la funzione sia non periodica lo spettro è continuo, e tanto più è esteso lungo l'asse delle frequenze quanto più è limitato nel dominio originario della variabile indipendente, e viceversa.
Nel caso in cui la funzione sia non periodica lo spettro è continuo, e tanto più è esteso lungo l'asse delle frequenze quanto più è limitato nel dominio originario della variabile indipendente, e viceversa. , dove
, dove  è l'
è l'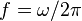 la frequenza delle sinusoidi di base la cui
la frequenza delle sinusoidi di base la cui