 Vi siete mai chiesti come funzionano i sintetizzatori musicali usati dai gruppi rock? Sentite il suono del moog della PFM in Impressioni di settembre. Come produce quel suono?
Vi siete mai chiesti come funzionano i sintetizzatori musicali usati dai gruppi rock? Sentite il suono del moog della PFM in Impressioni di settembre. Come produce quel suono?
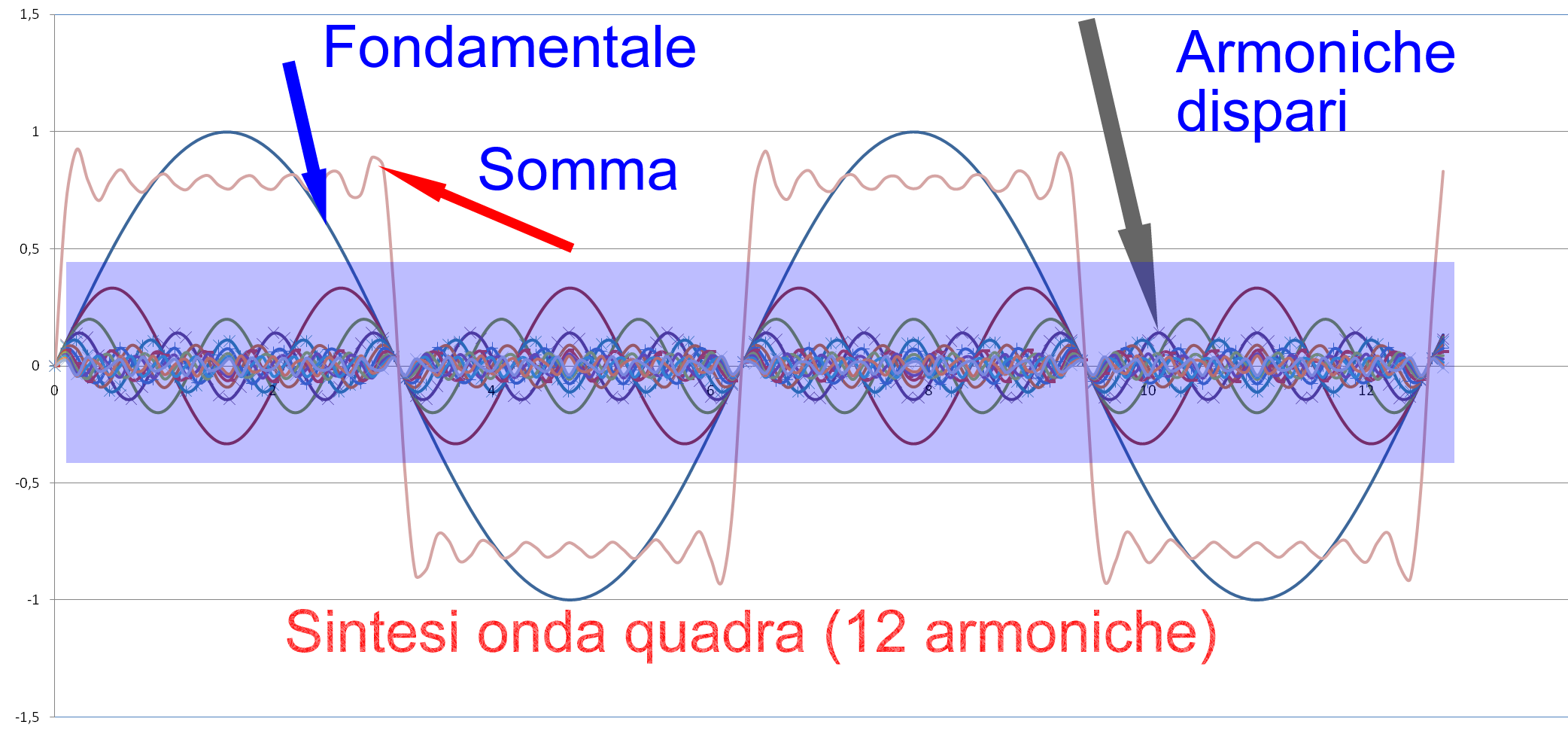
Lo strumento ha degli oscillatori, cioè dei circuiti che producono frequenze e la più semplice di esse è la sinusoide, che poi è il suono prodotto da un diapason. Fourier scoprì che se sommo in modo opportuno tali sinusoidi, posso "sintetizzare" qualunque forma d'onda corrispondente a qualsiasi strumento musicale. Io mi sono divertito a sintetizzare qualcosa di molto simile all'onda quadra, sommando alla frequenza fondamentale le sue armoniche dispari, cioè oscillazioni via via 3,5,7,9, ecc più alte ma con 3,5,7,9 ecc. ampiezze più basse. Il perchè di questo costituisce la teoria delle trasformate di Fourier. nella figura in alto in blu è la fondamentale le onde più piccole le armoniche, ne rappresento solo tre, mentre in viola è la somma delle 3,5,7,9,11,13, quindi 5 armoniche. Già con 10 di esse si ha un qualcosa di molto simile all'onda quadra.Se volete, ho il file excel.
(da Wikipedia).La trasformata di Fourier è largamente utilizzata nell'analisi in frequenza dei sistemi dinamici, nella risoluzione delle equazioni differenziali e in teoria dei segnali. Ad esempio, nell'ingegneria dei sistemi la trasformata di Fourier della risposta impulsiva caratterizza la risposta in frequenza del sistema in oggetto.
Il motivo di una così vasta diffusione risiede nel fatto che si tratta di uno strumento che permette di scomporre un segnale generico in una somma infinita di sinusoidi con frequenze, ampiezze e fasi diverse; e successivamente permette di ricostruirlo tramite la formula inversa di sintesi (o "antitrasformazione"). L'insieme di valori in funzione della frequenza, continuo o discreto, è detto spettro di ampiezza e spettro di fase.
Se il segnale in oggetto è un segnale periodico, la sua trasformata di Fourier è un insieme discreto di valori, che in tal caso prende il nome di spettro discreto o spettro "a pettine": la frequenza più bassa è dettaarmonica fondamentale ed è quella che ha peso maggiore nella ricomposizione finale del segnale, mentre le altre frequenze sono multiple della fondamentale e prendono talvolta il nome di "armoniche secondarie". In questo caso la rispettiva formula inversa di sintesi costituisce lo sviluppo in serie di Fourier della funzione o segnale periodico originario. Se il segnale ha un valor medio diverso da zero la serie restituisce anche una componente costante che lo rappresenta. Se un segnale periodico viene troncato all'esterno di un certo intervallo in ascissa rimanendo definito solo all'interno di un certo intervallo di definizione, lo spettro risultante sarà quello discreto in cui però ciascuna riga si allarga nel dominio della variabile dipendente di un valore pari all'inverso dell'intervallo di definizione del segnale stesso.
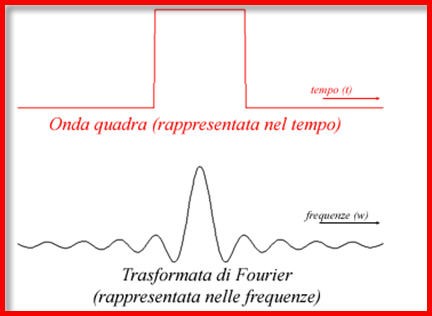 Nel caso in cui la funzione sia non periodica lo spettro è continuo, e tanto più è esteso lungo l'asse delle frequenze quanto più è limitato nel dominio originario della variabile indipendente, e viceversa.
Nel caso in cui la funzione sia non periodica lo spettro è continuo, e tanto più è esteso lungo l'asse delle frequenze quanto più è limitato nel dominio originario della variabile indipendente, e viceversa.
La teoria della trasformata e antitrasformata di Fourier generalizza dunque la teoria della Serie di Fourier al caso di segnali non periodici, ricomprendendo i segnali periodici come caso particolare ed insieme confluiscono nell'analisi di Fourier e nell'analisi armonica.
La trasformata di Laplace è un'estensione della trasformata di Fourier che è stata introdotta poiché consente di trattare funzioni particolari che non sono integrabili secondo Fourier, come le funzioni continue a tratti. Data la trasformata di Laplace di una funzione (o segnale), sotto determinate ipotesi si può ottenere la sua trasformata di Fourier ponendo  , dove
, dove  è l'unità immaginaria e
è l'unità immaginaria e 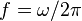 la frequenza delle sinusoidi di base la cui combinazione lineare determina la trasformata di Fourier.
la frequenza delle sinusoidi di base la cui combinazione lineare determina la trasformata di Fourier.

