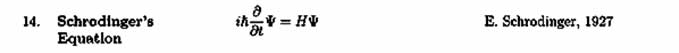

Parto dai miei appunti di quando ero studente: come potete vedere, questa equazione sembra una serie di caratteri scritti da un pazzo. E sembra diversa da quella in alto, ma non lo è. nell'equazione scritta in alto, H, è la cosidetta Hamiltoniana del sistema. Hamilton è un altro che si doveva fare i fatti suoi. Per farla breve, in H sono inserite derivate rispetto al tempo ed allo spazio. Dopo qualche calcolo si perviene a quella manoscritta. Per le date, non preoccupatevi.
Come si può notare questa è un'equazione d'onda, molto simile a quella riportata nell'articolo delle equazioni. Ma è un'onda strana ed esotica, che si muove nel campo dei numeri complessi, anzi in uno strano spazio, quello di Hilbert (sempre H!). Lo possiamo vedere anche dalla presenza di i a secondo membro le δ presenti stanno a significare "derivate parziali" rispetto ad una sola variabile, nel caso che ho una funzione, nel nostro caso Ψ che dipende sia dallo spazio che dal tempo. Solo il suo "modulo quadro" ha senso fisico diretto.
Il nostro problema è trovarla, dato il potenziale, l'energia potenziale della particella. Quando la si risolve, per dare senso fisico alle soluzioni, e non soltanto matematiche, e vi dico che è davvero complicato farno, anche in casi semplici, vien fuori una cosa del genere: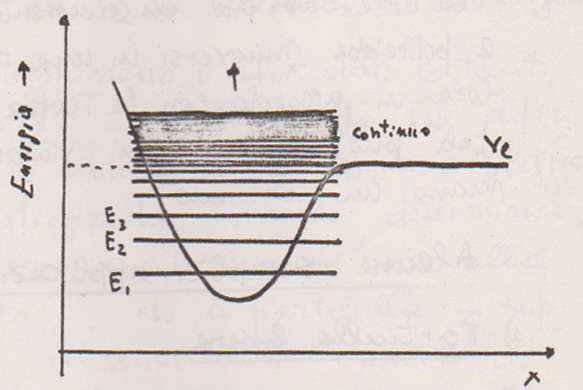
Cioè le energie permesse alla particella sono "quantizzate", non possono avere cioè qualsiasi valore, ma solo alcuni, fenomeno tanto più evidente quanto più è bassa l'energia.
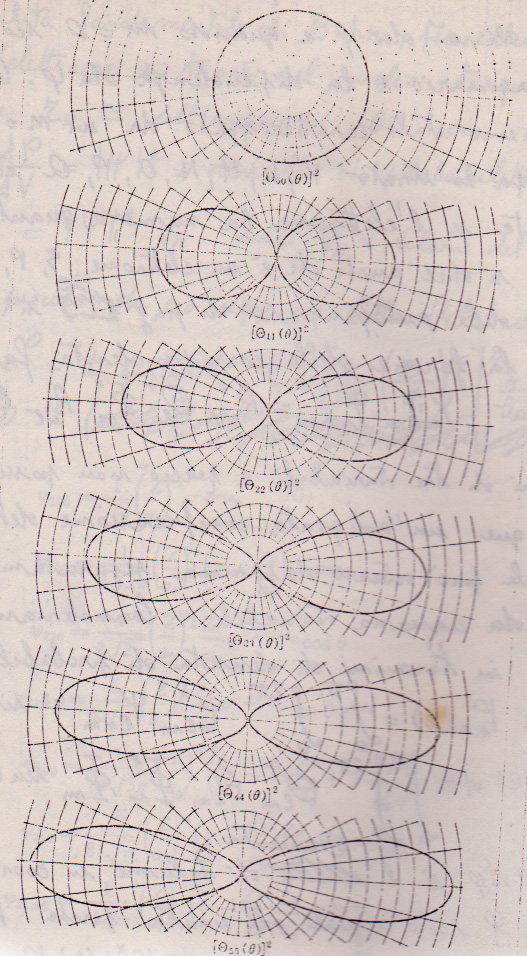
Con l'ausilio dei computers, il calcolo può essere fatto per interi atomi. Ad esempio, per l'atomo di idrogeno, posso calcolare le probabilià della posizione degli elettroni, trovando curve di questo tipo:
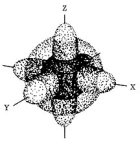
oppure, ancora più complicato(in 3d):
come si può vedere non tutte le zone dello spazio sono permesse. Dove è più scura, maggiore è la probabilità che ha l'elettrone di stare lì.